The Theory in Data Intelligence

The Multidisciplinary heuristics and theories that applies to Data Intelligence

By Ethan Yim

The Pareto Principle

The Pareto Principle, commonly known as the 80/20 Rule, is a recurring phenomenon across various fields. It suggests that a minority of causes (20%) often lead to the majority of results (80%). Conversely, the inverse holds true, where the remaining majority of causes (80%) contribute to a smaller portion of results (20%). The core idea is that a significant impact is driven by a minority of factors, emphasizing the non-uniform distribution of outcomes in diverse scenarios.

Background

Named after Italian economist Vilfredo Pareto, this principle originated from his observations in his own garden. His notable discovery was that a mere 20% of the pea pods were responsible for yielding 80% of the healthy peas. This realization extended beyond his garden, as he later found a similar pattern in the distribution of land ownership in Italy, where 80% of the land was possessed by only 20% of the population.

Purpose and Significance:

Purpose:

The Pareto Principle is a tool to help people become more productive and efficient with their time and resources.
It provides a rule of thumb (80/20 ratio) to identify the most important 20% of tasks/factors that generate the majority 80% of results.
By focusing time and effort on the vital 20%, you can get the greatest return on investment.
It encourages eliminating unproductive activities that waste time while only contributing minimally to outcomes.
The principle gives guidance on how to allocate time and resources optimally between the most impactful vs trivial factors.

Significance:

The Pareto distribution applies widely in many aspects of life and business, from economics to social relationships.
Recognizing this imbalance helps simplify priorities and separate the "signal from the noise".
It leads to higher productivity by zeroing in on the key leverage points that drive outcomes.
The principle promotes focus on quality (the vital 20%) over quantity of effort.
Applying the 80/20 rule allows you to work smarter, not just harder - do more with less.
It provides a simple but effective mental model to maximize results while minimizing wasted time and resources.

Real Life Examples

Chores

Around 80% of mess in a home often comes from 20% of items. For instance, clearing just a few clutter spots like the desk and sofa could make 80% of the house look tidy. Rather than exhaustively cleaning everything, focus on regularly maintaining those few high-impact areas.

Relationships

You likely get 80% of joy from 20% of personal relationships. Make time for the vital few friends and family who uplift you most. Don't spread yourself thin trying to please many casual acquaintances. Nurture the few core bonds that matter most.

Finances

Approximately 80% of spending may go to only 20% of expenses like housing, transportation and food. Identifying these biggest costs and budgeting smarter in those areas can greatly increase savings. Rather than penny-pinching everything, target the top 20% of expenditures to get the most fiscal benefit.

Issues

here's a common misconception about the Pareto principle—that with 20% effort, you'll achieve 80% of the results. It's essential to clarify that the 20% and 80% refer to causes and consequences, not effort percentages. The aim is not to minimize effort but to concentrate effort on a specific area for a more significant impact. Achieving 80% of results still requires giving 100% effort to that crucial 20%.

However, a potential drawback is team members becoming overly focused, neglecting other essential tasks. If you concentrate solely on the vital tasks, less important ones may be overlooked. Striking the right balance is key. Techniques like timeboxing or the Getting Things Done (GTD) method can help manage tasks effectively while leveraging the power of the 80/20 rule.

Connecting with Data Intelligence

Data Intelligence signifies the synergistic relationship between advanced data analytics (data science) and artificial intelligence, where intelligent systems leverage data-driven insights to make informed decisions, predictions, and automations.

Feature Selection

This principle has important implications in machine learning feature selection. It suggests that a small subset of features in the data may be responsible for the majority of the predictive signal.

Identifying these key predictive features allows for more efficient and interpretable models. Models built on fewer features are less prone to overfitting, faster to train, and easier to explain. The process of feature selection aims to find the minimal set of features that contains the most predictive power.

Various techniques can identify the vital few features. Filter methods like correlation coefficients and statistical tests assess features independently. Wrapper methods like recursive feature elimination use the model performance itself to evaluate feature sets. Embedded methods perform feature selection as part of the model construction process itself.

Once the most influential features are found, the remaining negligible features can be ignored without substantially sacrificing model accuracy. Focusing modeling efforts on the vital features instead of all available features allows for great simplification.

Example: In a predictive maintenance model for manufacturing equipment, features like operating temperature, vibration levels, and historical maintenance records might constitute the vital 20%. Focusing on these factors enables the creation of a more efficient model for predicting equipment failures.

Data Cleaning and Preprocessing

In machine learning, dirty data can severely degrade model performance. Data cleaning and preprocessing aims to detect and fix issues like missing values, duplicates, errors, and inconsistencies. However, not all data problems impact models equally.

The Pareto Principle suggests that data quality issues may follow an 80/20 rule - 80% of the problems originate from 20% of the data. A few "dirty" features or records could be responsible for the majority of errors. Targeting the correction of these crucial problems can lead to an outsized improvement in overall data quality.

Tools like visualization, summary statistics, and outlier detection can identify the most problematic parts of the data. Data cleaning efforts should prioritize fixing issues in the vital subset of dirty data first. Techniques like imputation, normalization, and record matching can then correct the key problems.

With the significant data quality issues resolved, smaller problems in the remaining majority of the data can be safely ignored. The Pareto Principle highlights that data cleaning is not uniformly important across all data points. A targeted approach focused on the critical minority of issues enables efficient preprocessing leading to greatly enhanced data quality.

Example: Consider a customer database for an e-commerce platform; a small subset of customer records might have inconsistent entries in address fields. Prioritizing the cleaning of this subset ensures that customer segmentation and analysis are based on accurate and reliable data.

Resource Optimization

Data science projects often deal with large datasets and complex models that require substantial computational resources. However, the Pareto Principle suggests that much of the insights or predictive power may come from a small critical subset of the data and parameters.

For example, 80% of a model's accuracy may depend on just 20% of its features. Or, 80% of the training time could be spent adjusting 20% of the weights. Identifying and focusing on these vital components is key for resource optimization.

Techniques like feature selection, dimensionality reduction, and parameter pruning can isolate the important minority of data and model factors. Computational effort can then be allocated more heavily towards these critical components compared to negligible ones.

For instance, training may utilize more epochs focused on adjusting the most influential 20% of weights rather than spreading effort evenly. Or more ensemble members could be assigned to high-impact features. The Pareto Principle guides the selective application of resources to maximize overall efficiency and project results.

By targeting computational power at the minority of components that offer the greatest leverage, data science teams can optimize resource usage while still capturing most of the available value.

Example: In training a machine learning model for sentiment analysis, focusing on a small subset of hyperparameters related to feature selection and model architecture can lead to quicker training times without compromising accuracy.

Error Analysis

When evaluating model performance, the Pareto Principle suggests that a minority of errors may be responsible for the majority of the inaccuracy. Not all mistakes impact the model equally.

Tools like confusion matrices, error reports, and residual plots can identify the vital errors that have an outsized influence. Common major errors include those from significant data subsets, highly weighted parameters, or under-performing modules.

Analyzing and addressing these high-impact errors is crucial for efficient model improvement. Techniques like tweaking loss functions, targeted data augmentation, and component tuning can help resolve the major errors.

Meanwhile, minor residual errors that have little effect can be safely ignored without much loss in overall performance. The Pareto Principle focuses error analysis efforts on the critical minority of mistakes in order to maximize improvements in accuracy.

Prioritizing the correction of the most significant errors allows for an effective refinement of the model. Rather than uniformly reducing all errors, which results in diminishing returns, targeted error analysis guided by the 80/20 rule achieves greater enhancement of model performance.

Example: In a medical diagnostic model, misclassifying severe conditions might have more severe consequences. Focusing on reducing errors related to critical conditions ensures a more robust and reliable diagnostic tool.

Business Impact

In business, outcomes are driven by many diverse factors. However, the Pareto Principle suggests that 80% of results often stem from 20% of the causes. Key elements like high-value customers, best-selling products, and critical processes underpin overall performance.

Identifying these vital few drivers allows businesses to optimize operations and strategy. Efforts can concentrate on the minority of factors that offer the greatest leverage on overall results.

For example, customer segmentation may find 20% of customers generate 80% of revenue. Focusing marketing on these core customers has an outsized impact on sales. Production might prioritize the 20% of products delivering the most profit. Enhancing the key processes that facilitate core operations also provides substantial gains.

By allocating resources and talent towards the critical minority of drivers, businesses can maximize returns on investment. The Pareto Principle provides perspective on how outsized results do not require uniform efforts across all factors. Instead, businesses should identify and focus on the vital few.

Example: In retail, a small percentage of products might contribute significantly to profit margins. By prioritizing inventory management and marketing for these high-impact products, a business ensures a more profitable and sustainable strategy.

Decision-Making

Making sound decisions relies on having quality information. However, the Pareto Principle suggests that not all available information will be equally useful. Typically, 20% of information drives 80% of decision outcomes.

Identifying this vital 20% allows for more focused and analytical decision-making. Tools like influence diagrams, value of information analysis, and predictive modeling can help determine the most decision-relevant information.

For example, in financial analysis, current profit margins and expected growth rates may be most informative for valuation. Or in risk assessment, the likelihood and impact of the top risks might shape mitigation priorities.

Focusing efforts on gathering and examining the minority of factors with the greatest informational impact improves decision quality and efficiency. Meanwhile, extraneous data that has little sway on outcomes can be set aside.

The Pareto Principle serves as a guide for extracting key insights from the wealth of information. By concentrating on the critical subset of decision-driving information, choices can be made analytically rather than heuristically.

Example: In a financial investment decision, focusing on economic indicators and market trends that have historically had a significant impact on asset performance ensures more informed decision-making.

Algorithmic Efficiency

In machine learning, many algorithms can be applied to a given problem. However, their performance may follow an 80/20 rule - 80% of the best results come from just 20% of the algorithms. Certain algorithms excel in diverse situations.

Identifying this vital top-performing 20% allows data scientists to focus their efforts. Algorithm selection can start with the critical few contenders known to generally work well. Hyperparameter tuning also concentrates on optimizing the key algorithms.

For example, random forests and gradient boosting machines often feature among the top machine learning algorithms. Bayesian methods frequently outperform in uncertainty quantification. Focusing efforts on tuning and tweaking these consistently excellent algorithms improves overall outcomes.

Meanwhile, algorithms that rarely provide top results across problem types can have selections and computations streamlined or omitted without much performance sacrifice. The Pareto Principle provides perspective that while many options exist, a few vital choices deserve priority.

By directing attention towards algorithms empirically demonstrated to reliably perform well, data scientists can make efficient and effective modelling choices. The critical minority of superior algorithms merits greater focus to maximize gains.

Example: In natural language processing tasks, a small subset of algorithms might excel in sentiment analysis. Focusing on optimizing these algorithms enhances the efficiency of the entire natural language processing pipeline.

Time Management

Data science projects entail many diverse tasks from data cleaning to model building. With limited time, the Pareto Principle suggests focusing efforts on the vital 20% of tasks that drive 80% of the project outcomes.

Prioritizing the key tasks with the greatest impact ensures efficient time utilization. Techniques like critical path analysis, agile sprints, and Pareto analysis help identify the most critical tasks.

For example, building the core machine learning model that powers the product may be far more important than tweaking auxiliary visualizations. Or properly validating the model on real-world data likely takes priority over stress testing edge cases.

Focusing effort on the minority of tasks central to project success has an outsized impact. The remaining less-critical tasks can be deprioritized, simplified or deferred.

The Pareto Principle provides perspective on selectively applying effort to the few major tasks that truly move the project forward. By concentrating on the essential 20% of work, data scientists can drive 80% of the outcomes while prudently managing time.

Example: In a data exploration phase, spending more time on understanding and visualizing the critical patterns in the data ensures a more insightful analysis. Prioritizing this aspect allows for more effective subsequent model development.

How would a Data Scientist know what the most important parts are?

Domain Understanding: Knowledge Acquisition: Gain a deep understanding of the problem domain. Engage with subject matter experts to identify key variables or factors that are likely to have a significant impact on the outcome.

Exploratory Data Analysis (EDA): Feature Importance Techniques: Employ techniques such as feature importance analysis to understand the contribution of each variable to the target variable. Methods like permutation importance, tree-based methods, or model-agnostic approaches like SHAP (Shapley Additive explanations) can provide insights into variable importance.

Correlation Analysis: Explore the interrelationships between variables. Identify pairs or groups of variables that exhibit strong correlations, as these might collectively represent a crucial subset.

Visualization: Use data visualization tools to identify patterns and outliers. Visual representations can often reveal the most impactful features or patterns within the data.

Model Evaluation and Iteration: Model Performance Metrics: Assess the performance of the model using relevant metrics. Identify variables that consistently contribute to model performance. This can be achieved through techniques like recursive feature elimination or stepwise regression.

Cross-Validation: Perform cross-validation to ensure the stability and generalizability of the model. Features that consistently appear in the optimal models across different folds are likely to be part of the critical subset.

Business Impact Assessment: Business-Relevance Criteria: Evaluate variables based on their potential impact on business outcomes. Consider the downstream consequences of including or excluding certain variables in terms of actionable insights and decision-making.

Iterative Refinement: Feedback Loops: Establish feedback loops with stakeholders, subject matter experts, and end-users. Iterate on model development based on their insights and feedback, ensuring alignment between model outputs and real-world impact.

Experimentation: A/B Testing: If applicable, conduct A/B testing or controlled experiments to assess the impact of specific variables on the desired outcomes. This empirical approach helps validate the importance of variables in a real-world context.

Continuous Monitoring: Model Monitoring: Implement continuous monitoring of model performance in production. If variables are dynamic or subject to change, regularly reassess their importance and update the model accordingly.

Ensemble Methods: Ensemble Model Techniques: Explore ensemble methods that combine multiple models. Ensemble techniques, such as stacking or bagging, can reveal the consensus among models regarding the importance of different variables.

Text over media

Cognitive Dissonance Theory

Cognitive Dissonance Theory is a psychological concept that delves into the discomfort individuals experience when holding conflicting beliefs or attitudes. It plays a crucial role in understanding decision-making processes, belief systems, and the quest for internal consistency.

Background

This theory emerged from the work of psychologist Leon Festinger in the mid-20th century. Festinger observed that when individuals hold contradictory beliefs or engage in behaviors misaligned with their values, they experience a psychological discomfort known as cognitive dissonance.

Purpose and Significance

Purpose:

Internal Consistency: Cognitive Dissonance Theory aims to explain the human tendency to seek harmony in their thoughts and actions. It highlights the discomfort arising from conflicting beliefs, pushing individuals toward resolving the dissonance.
Motivation for Change: The theory posits that individuals are motivated to reduce cognitive dissonance, leading to adjustments in beliefs or behaviors. This serves as a powerful driving force for personal development and change.
Understanding Decision-Making: Cognitive Dissonance Theory helps unravel the intricacies of decision-making. When faced with conflicting options, individuals strive to align their choices with their existing beliefs to alleviate discomfort.

Significance:

Behavioral Insights: Cognitive Dissonance Theory provides valuable insights into human behavior, explaining why individuals may modify their attitudes or opinions to align with their actions, even if those actions contradict their initial beliefs.
Marketing and Persuasion: Marketers often leverage cognitive dissonance to influence consumer behavior. Understanding that individuals seek consistency, marketers can frame messages to align with consumers' existing beliefs, reducing the likelihood of dissonance.
Conflict Resolution: In interpersonal relationships, recognizing and addressing cognitive dissonance can aid in resolving conflicts. Acknowledging the discomfort and working towards alignment can foster healthier interactions.
Learning and Growth: Cognitive Dissonance Theory underscores the role of discomfort in prompting learning and growth. Embracing cognitive dissonance as a natural part of intellectual development encourages individuals to confront and adapt to new information.
Decision-Making Strategies: Individuals can apply the principles of cognitive dissonance to make more informed decisions. By understanding the potential for discomfort in holding conflicting beliefs, people can approach choices with greater self-awareness.

Real World Examples

Smokers

Smokers who learn about the strong evidence linking smoking to lung cancer experience cognitive dissonance between their behavior (smoking) and this new information. They may try to reduce dissonance by questioning the evidence, downplaying the risks, or telling themselves they will quit soon.

Bias

A person who identifies as unbiased but then encounters evidence of biases within themselves experiences dissonance between their self-image and this information. They may reduce it by critiquing the research methodology, denying personal bias, or adjusting their views of objectivity.

Meat Eaters

An animal lover who eats meat feels dissonance between caring about animals and eating them. They may reduce dissonance by saying humans need meat, believing regulations protect farm animals, or compartmentalizing pets versus livestock.

Issues

Feels Different for Everyone: Dissonance, or that uncomfortable feeling when things don't match up, is different for each person. It's like how some people might find certain foods weird while others love them.
Not Clear What It Really Means: Understanding dissonance is a bit like trying to figure out a tricky puzzle. People might not agree on exactly what it is, just like friends might see a picture differently.
We're All Different: Imagine a group of friends reacting to a funny joke. Some might laugh a lot, while others just smile. That's because everyone responds to dissonance in their own way, just like how friends react differently to jokes.
Not Like Real Life Sometimes: Think of dissonance experiments like cool science experiments in class. But sometimes, these experiments are like doing a science project about aliens when what we really want to know is how to make awesome slime at home. Real-life situations can be different from these experiments.
Not Everyone Gets to Play: Imagine playing a game, but only some friends get to join. That's like how some experiments only include certain types of people, and it might not represent what happens with everyone in the real world.

Connecting with Data Intelligence

Identification of Discrepancies

Theory: Cognitive dissonance arises when individuals become aware of conflicting beliefs or attitudes.
Data Intelligence: Advanced analytics and algorithms can identify discrepancies and patterns within vast datasets, bringing attention to areas of inconsistency or contradiction

Informed Decision-Making

Theory: Individuals seek to reduce dissonance by aligning beliefs with actions.
Data Intelligence: Decision-makers can use comprehensive and coherent data insights to align organizational strategies with accurate information, enabling more informed and effective decision-making.

Continuous Improvement

Theory: Individuals adjust beliefs to minimize discomfort.
Data Intelligence: Data professionals continually refine data practices, implementing feedback loops, and adapting methodologies to improve the consistency and reliability of data over time.

Data-Driven Problem-Solving

Theory: Cognitive dissonance motivates resolving inconsistencies for effective problem-solving.
Data Intelligence: Data-driven problem-solving relies on addressing and resolving inconsistencies in the data, leading to more effective solutions.

Enhancing User Trust

Theory: Resolving cognitive dissonance builds trust and confidence.
Data Intelligence: Ensuring data accuracy and addressing inconsistencies enhances user trust, encouraging stakeholders to rely on data-driven insights for decision-making.

Strategic Adaptation

Theory: Inconsistencies impact organizational strategies.
Data Intelligence: Organizations can adapt strategies based on accurate and consistent data, aligning with the dynamic insights derived from ongoing analysis.

Predictive Analytics for Change

Theory: Anticipating future inconsistencies can motivate change.
Data Intelligence: Predictive analytics models can forecast potential data inconsistencies or emerging patterns, enabling proactive measures and strategic interventions for positive change.

Communicate Finding

Theory: Communicating resolutions is essential in dissonance reduction.
Data Intelligence: Clear and transparent communication of data findings ensures that stakeholders understand the resolutions to inconsistencies, fostering a collaborative environment for change.

Benford's Law

Benford's Law, also known as the first-digit law, reveals fascinating insights into the psychology of numerical patterns and expectations. In simple terms if you had a set of numbers, 10, 1000, 23, 25, 90, 8, 86594, 213782345, the first digit of every number should apply to the law.

Background:

Named after physicist Frank Benford, this law observes the non-uniform distribution of first digits in many datasets. It originated from Benford's curiosity about the frequency of the first digits in diverse sets of numerical data.

Purpose and Significance:

Purpose:

Numerical Perception: Purpose: Benford's Law sheds light on how individuals perceive and expect numerical patterns. The tendency for certain digits to appear more frequently as leading digits reflects cognitive processes in numeric interpretation.
Detecting Anomalies: Purpose: In data analysis, Benford's Law is employed to identify anomalies or irregularities. Deviations from the expected distribution may signal errors, fraud, or inconsistencies in datasets.
Psychological Implications: Purpose: The law serves to uncover psychological aspects of how people naturally generate or encounter numerical data, influencing their mental models of numeric frequencies.

Significance:

Cognitive Biases: Significance: Benford's Law highlights cognitive biases in how individuals intuitively expect numerical distributions. Understanding these biases is crucial for accurate data interpretation and analysis.
Data Authenticity: Significance: In fields like forensic accounting or fraud detection, Benford's Law is significant for assessing the authenticity of numerical datasets. It acts as a tool to flag suspicious patterns.
Algorithmic Applications: Significance: The law has applications in algorithmic analysis, especially in artificial intelligence. Algorithms leveraging Benford's Law can enhance anomaly detection and improve data quality assessments.

Real World Example

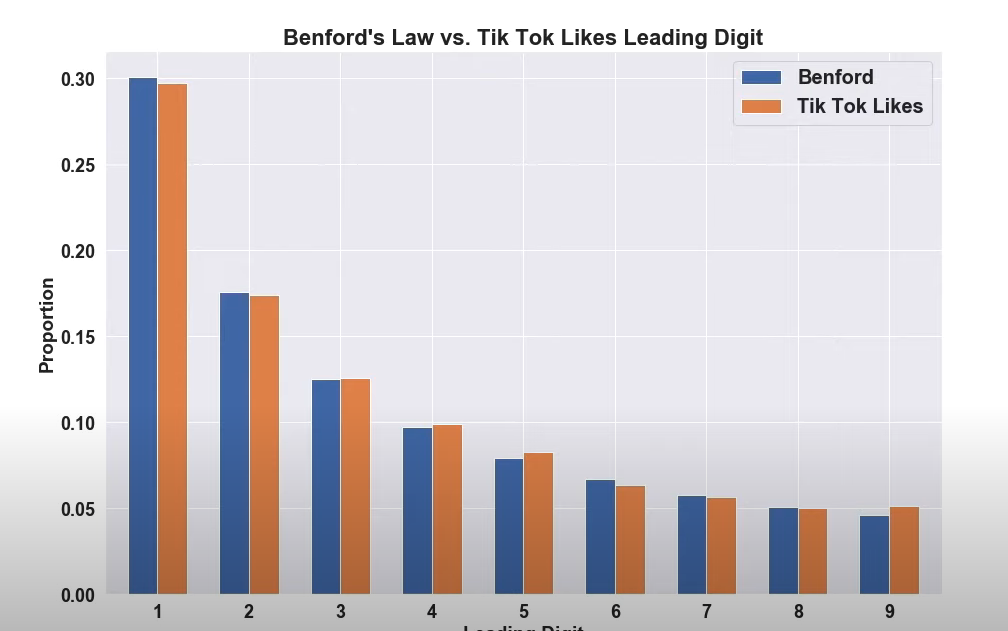
This user used Benford's Law and determined if it applied to the number of likes on TikTok videos posted on their FOR YOU page. The researchers are trying to test if the first few digits in TikTok video likes follow a special pattern, which is known as the Benford's Law. The results of the research showed a surprising resemblance between the predicted distribution based on the Benford's law and the actual distribution of front numbers in TikTok likes, as shown in an image of an orange bar chart. Even though there were slight differences, such as the way the digit 9 looked, the overall pattern indicated that Benford's Law could be applied to TikTok likes data.

Connecting with Data Intelligence

Fraud Detection

Benford's Law is a potent tool for detecting anomalies and potential fraud in datasets.
Application in Data Science/AI: Data scientists and AI algorithms can leverage Benford's Law to identify irregularities in financial or transactional data, aiding in the early detection of fraudulent activities.

Data Quality Assessment

Benford's Law serves as a quick and effective means to assess the integrity and quality of large datasets.
Application in Data Science/AI: Data scientists can use Benford's Law to evaluate the distribution of leading digits, ensuring the reliability of input data for machine learning models and analytics, thus improving overall data quality.

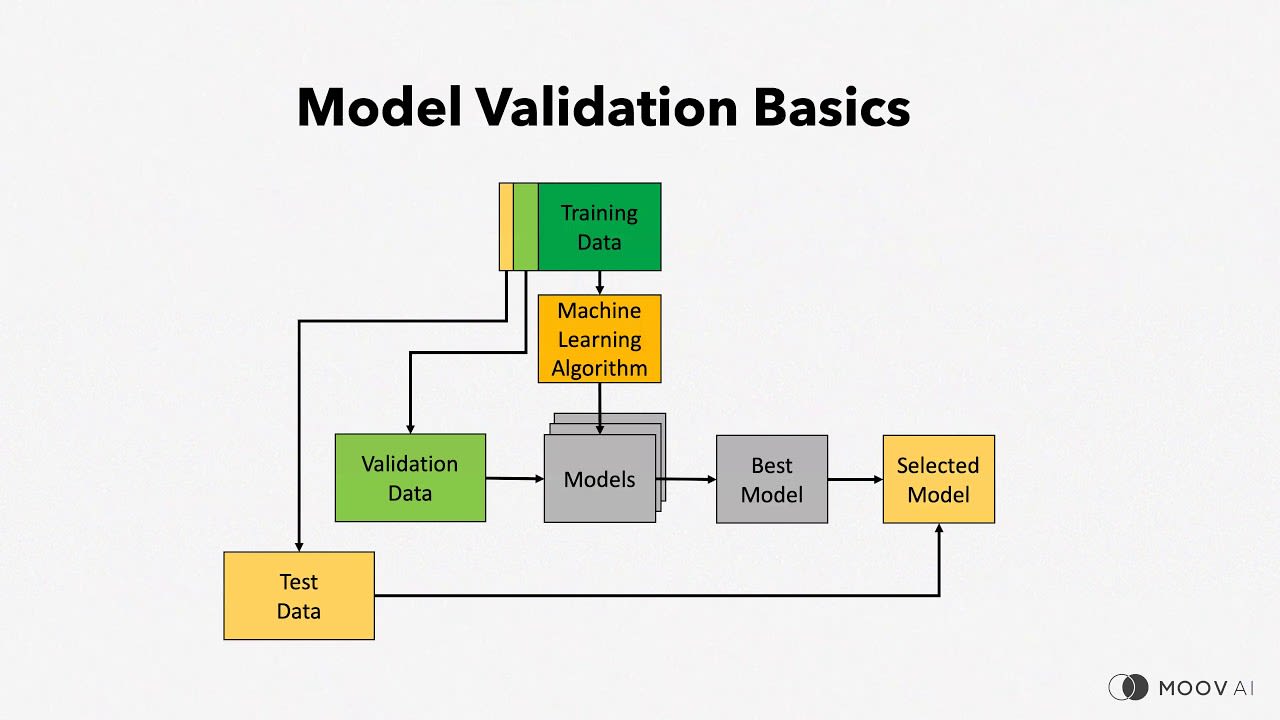
Algorithmic Testing and Validation

Benford's Law can be applied to assess the outputs of algorithms or computational models.
Application in Data Science/AI: Data scientists and AI practitioners can use Benford's Law to validate the results produced by algorithms, helping identify potential issues with the algorithm's implementation or input data, ensuring the accuracy of AI-generated insights.

Continuous Monitoring for Data Streams

Benford's Law can be used for continuous monitoring to ensure ongoing adherence to statistical principles.
Application in Data Science/AI: AI models can incorporate Benford's Law checks as part of continuous monitoring systems, providing real-time alerts when deviations occur in the data streams used for model training or evaluation. This ensures the reliability of AI models over time.

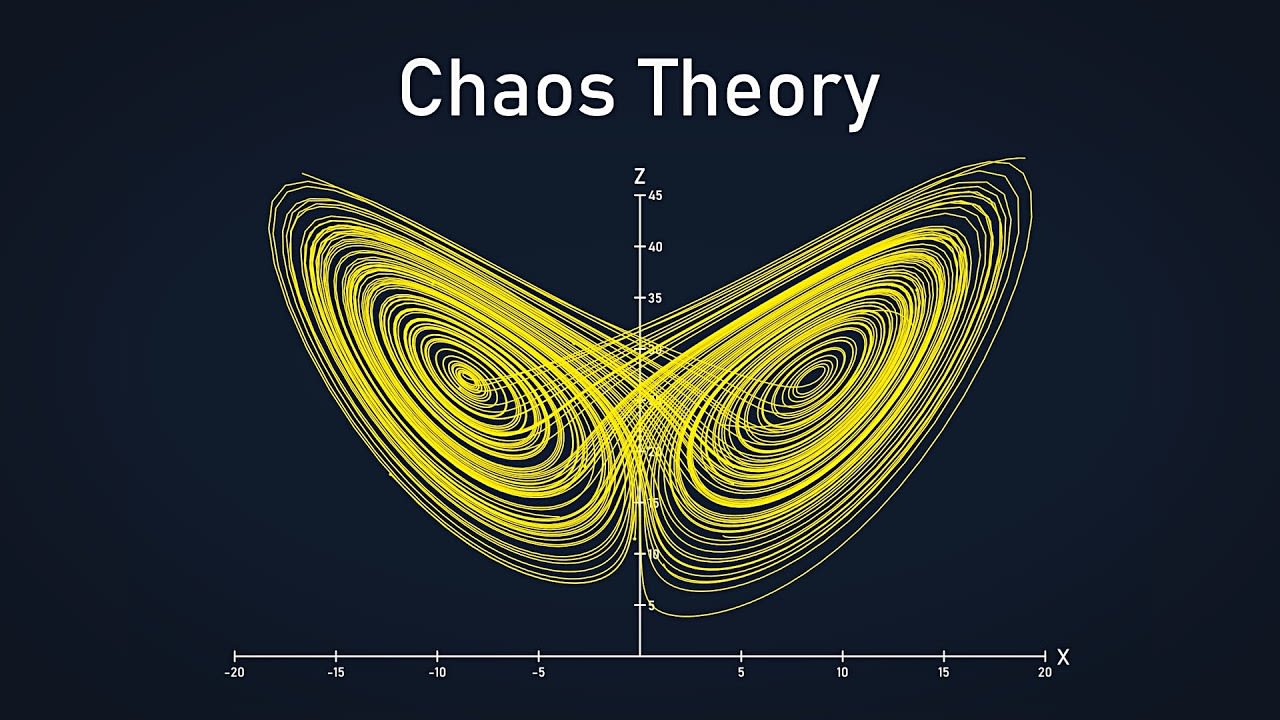
Chaos Theory

Chaos Theory is a fascinating concept that explores the unpredictable nature of complex systems and how small changes can lead to significant and seemingly random outcomes. It plays a crucial role in understanding the dynamics of various phenomena, from weather patterns to the behavior of dynamic systems.

Background

This theory emerged as a branch of mathematics and physics, gaining prominence in the latter half of the 20th century. Chaos Theory delves into the idea that deterministic systems, despite being governed by precise laws, can exhibit unpredictable behavior over time.

Purpose and Significance

Purpose:

Unpredictability in Complexity: Chaos Theory aims to unravel the inherent unpredictability within complex systems. It highlights how minor alterations in initial conditions can lead to vastly different outcomes, emphasizing the sensitivity of dynamic systems.

Understanding Dynamic Systems: The theory provides valuable insights into the behavior of dynamic systems, where seemingly chaotic patterns can emerge from deterministic processes. This understanding is essential in fields ranging from physics to biology.

Emergence of Patterns: Chaos Theory explores the emergence of patterns in apparently disorderly systems. It sheds light on how intricate structures and behaviors can arise spontaneously, offering a deeper understanding of the underlying order in chaos.

Significance:

Informed Decision-Making: Chaos Theory encourages a nuanced perspective on decision-making in complex situations. Recognizing the potential for unpredictability, individuals and organizations can make more informed decisions by considering the dynamic nature of the systems involved.

System Resilience: Understanding chaos and unpredictability in systems allows for the development of strategies that enhance resilience. By anticipating potential variations and disturbances, systems can better adapt to changing conditions.

Scientific Exploration: Chaos Theory has profound implications for scientific exploration, challenging traditional notions of determinism. It opens new avenues for understanding phenomena like turbulence, population dynamics, and neural networks.

Innovation and Creativity: Embracing chaos can foster innovation and creativity. By acknowledging the potential for unpredictability, individuals can explore novel ideas and approaches, recognizing that order can emerge from apparent disorder.

Dynamic Adaptation: Chaos Theory underscores the importance of dynamic adaptation. Systems that can adjust and evolve in response to changing conditions are better equipped to navigate the inherent chaos present in various natural and artificial environments.

Challenges:

Unpredictability: Chaos theory emphasizes the sensitivity to initial conditions, implying that small changes can lead to vastly different outcomes. In data science, this can pose challenges when dealing with complex models where slight variations in input data or parameters might result in significantly different predictions.
Nonlinear Dynamics: Many real-world phenomena, especially in AI and data science applications, are inherently nonlinear. While this complexity allows for modeling intricate relationships, it also makes it challenging to interpret and predict system behavior accurately.
Modeling Complex Systems: Chaos theory often deals with highly complex systems, and modeling such systems accurately can be difficult. Machine learning models might struggle to capture and represent the intricate dynamics of chaotic systems.

Benefits:

Pattern Recognition: Chaos theory can aid in recognizing patterns in seemingly random or complex data. It introduces concepts like strange attractors and fractals that help identify underlying structures, leading to improved pattern recognition and feature extraction.
Understanding Nonlinear Relationships: In data science, many real-world relationships are nonlinear. Chaos theory provides a framework for understanding and dealing with nonlinear dynamics, enabling the development of more accurate models for complex systems.
Adaptability: Chaos theory underscores the importance of adaptability in complex and dynamic environments. This principle is relevant in AI and machine learning, encouraging the development of models that can adapt to changing conditions and evolving data.
Anomaly Detection: Chaos theory's focus on detecting irregularities and bifurcations can be applied in data science for anomaly detection. Identifying critical points of change in data patterns is crucial for detecting outliers or unusual behavior.

Connecting with Data Intelligence

Weather Prediction

Chaos theory's Butterfly Effect highlights the sensitivity of dynamic systems to initial conditions. Weather systems exhibit chaotic behavior, making long-term predictions challenging.

Application: In meteorology, chaotic behavior in the atmosphere requires sophisticated data intelligence models. Numerical weather prediction relies on complex algorithms to assimilate vast amounts of data, considering the chaotic nature of the atmosphere to provide more accurate short-term weather forecasts.

Financial Markets

Connection: Financial markets are dynamic and influenced by numerous factors. Chaos theory's emphasis on nonlinear dynamics aligns with the intricate and often unpredictable behavior of financial systems.

Application: Data intelligence is crucial in financial modeling and algorithmic trading. Chaos theory concepts guide the development of models that account for the nonlinear relationships in market data, helping traders make informed decisions in dynamic and uncertain market conditions.

Epidemiology and Disease Spread

Connection: The spread of diseases in populations can exhibit chaotic behavior due to factors like individual interactions and environmental conditions. Small changes in these variables can lead to significant differences in disease outcomes.

Application: Data intelligence plays a pivotal role in modeling disease spread and predicting outbreaks. Chaos theory informs the development of models that consider the sensitivity to initial conditions, allowing for better understanding and management of infectious diseases.

Conclusion

These concepts are incredibly useful in data science and artificial intelligence fields. It is fascinating to see how these theories have been applied to the real world and how beneficial it is.

The Pareto Principle:
Benefit: By identifying the 20% of things that really matters, it helps students to be more efficient and focused on their studies.
Impact: In simple words, it helps people to manage their time and work more efficiently.

Cognitive Dissonance Theory:
Benefit: Helps explain why people do the things they do and how they make choices.
Impact: So AI design becomes more user-friendly and effective. It makes the speeches, advertisements, and discussions more convincing which lead to better outcomes.

Benford's Law:
Benefit: It helps in tracking the fraud, evaluating the accuracy of the data and comparing it with other companies.
Impact: It increases accuracy by detecting abnormalities and inconsistencies in data. It contributes to improving algorithmic testing, early detection of data anomalies, and ensuring data credibility, which are crucial aspects of AI and machine learning.

Chaos Theory:
Benefit: Explain to me about the topic in simpler terms.
Impact: It helps to create better models of dynamic events like the weather, financial markets and disease spread. In the field of data science and AI, we use techniques such as regularization and cross-validation to guide model development. This ensures that the models take into account nonlinear relationships, resulting in improved predictions and better decision-making.

By learning and applying these theories we become proficient in handling and interpreting complex data effectively. Combining different approaches will help us to get a balanced view of the field and give us the ability to create unique solutions that are better suited to different situations.

Process

Here is the process and the references!